Unit 1 DSA AKTU NOTES [[FREE]] | Aktu DSA Notes | Data Structure and Algorithm Completely Free Notes | AKTU FREE NOTES

 UNIT 1 

Introduction:

1. Basic Terminology:

• Understanding these terms is crucial for grasping more advanced concepts.

• • Variable: A named storage location in a computer's memory that can hold different values during program execution. Example: int x;
  • Constant: A value that does not change during the execution of a program. Example: const int PI = 3.14;
  • Data: Facts, statistics, or information that can be processed. Examples: numbers, text, images.
  • Algorithm: A finite sequence of well-defined, computer-implementable instructions to solve a specific problem. Example: Sorting an array using the Bubble Sort algorithm.

2. Elementary Data Organization:

• Definition: Elementary Data Organization involves the foundational principles of how data is structured at its most fundamental level. This understanding is vital for selecting appropriate data structures and optimizing algorithms.

• 
  

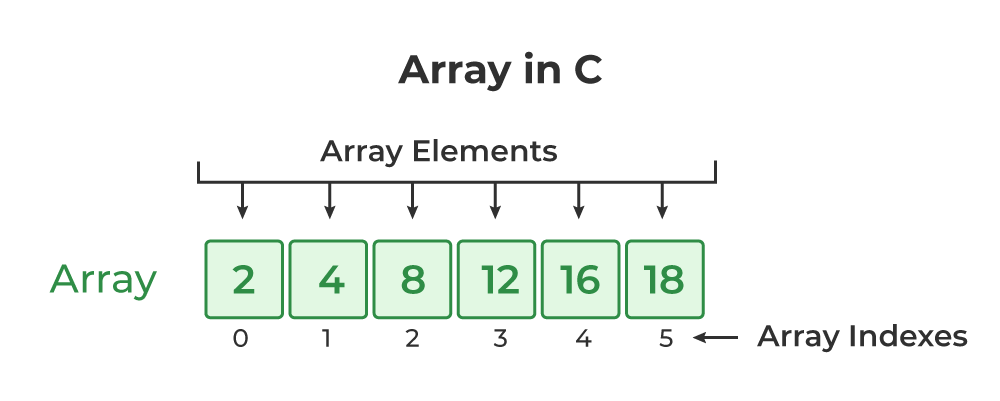
• Array: An array is a fixed-size, contiguous memory structure that stores elements of the same data type. Elements are accessed using an index, allowing for direct and constant-time access. For example, in the array int numbers[5] = {1, 2, 3, 4, 5};, accessing the third element is achieved through numbers[2], yielding the value 3.

  Linked List: A linked list is a dynamic data structure where elements, called nodes, are connected via pointers, forming a linear sequence. Nodes hold data and a reference to the next node in the sequence. For instance, in the singly linked list Node 1 -> Node 2 -> Node 3 -> null, each node points to the next, facilitating efficient insertions and deletions.

  Tree: A tree is a hierarchical data structure comprising nodes connected by edges. Each node has a value, and nodes may have children. A binary tree, for example, has at most two children per node. In the binary tree:

• 

  Credit: GeeksforGeeks

  
  Node 1 is the root, nodes 2 and 3 are its children, and so on. Trees are versatile for representing hierarchical relationships and recursive structures.

• 3. Built-in Data Types in C:

  Definition: Built-in data types in C refer to the primitive data types that are predefined in the C programming language. These data types are the fundamental building blocks for storing and manipulating different kinds of values in a C program.

• Examples:

1. int (Integer): Used to store whole numbers, both positive and negative, without decimal points. Example: int age = 25;

2. float (Floating-Point): Used to store real numbers with single precision, including decimal points. Example: float pi = 3.14;

3. char (Character): Used to store a single character. Example: char grade = 'A';

• Algorithm Definition:

  1. Definition: An algorithm is a systematic, step-by-step procedure or set of rules for solving a computational problem. It represents a clear and unambiguous set of instructions that, when followed, lead to the solution of a specific task or objective. Algorithms are fundamental to computer science and programming as they provide a structured approach to problem-solving.

  2. Properties:

  • Input: An algorithm takes input from a specified domain, which could be a set of values, variables, or any form of data that the algorithm operates on.
  • Output: It produces a well-defined output, a result, or a solution based on the given input. The output is related to the nature of the problem being solved.
  • Definiteness: Each step in the algorithm must be precisely and unambiguously defined. There should be no room for interpretation or confusion about what each step entails.
  • Finiteness: The algorithm must terminate after a finite number of steps, meaning it should not run indefinitely. This ensures that the problem-solving process reaches a conclusion.
  • Effectiveness: The algorithm should be practical and feasible, meaning it can be executed using available resources within a reasonable amount of time. It should be efficient in solving the problem it addresses.

Examples:

• 1. Linear Search Algorithm:

• Definition: Given a list of elements, find a specific element by checking each one in order.
• Properties: Takes a list as input, produces the position of the desired element as output, each step is well-defined and finite.
• 
  

• 2. Bubble Sort Algorithm:

• Definition: Sort an array of elements by repeatedly swapping adjacent elements if they are in the wrong order.
• Properties: Takes an array as input, produces a sorted array as output, each step is well-defined and finite.

Efficiency of an Algorithm:

1. Time Complexity:

• Definition: Time complexity is a measure of the total time an algorithm takes to complete as a function of the input size. It quantifies the efficiency of an algorithm by estimating the number of basic operations it performs in relation to the input size.
• Factors Influencing:
  • Input Size: As the size of the input data increases, the time complexity may also increase.
  • Hardware: Different hardware may affect the execution speed of algorithms.
  • Software Environment: The efficiency of algorithms can be influenced by the programming language and the underlying software environment.

Example: Linear Search Algorithm:

• Explanation: In the linear search algorithm, the time complexity is O(n), where 'n' is the size of the input array. The algorithm iterates through the array once, checking each element until it finds the target or reaches the end. The time taken is directly proportional to the size of the input array.

2. Space Complexity:

• Definition: Space complexity is a measure of the total memory space an algorithm uses as a function of the input size. It assesses the efficiency of an algorithm by estimating the amount of additional memory required for its execution.
• Factors Influencing:
  • Data Structures: The choice of data structures impacts the space complexity.
  • Recursion: Recursive algorithms may consume additional memory for each recursive call.
  • Auxiliary Space: Extra space used for temporary storage or variables.

Example: Merge Sort Algorithm:

Explanation: In the merge sort algorithm, the space complexity is O(n), where 'n' is the size of the input array. This space is used for creating temporary arrays during the merging process. The algorithm divides the array into halves recursively, requiring additional space for each recursive call.

Asymptotic Notation Explained with Examples:

1. Big Oh (O):

• Definition: Big Oh (O) notation provides an upper bound or worst-case scenario for the growth rate of an algorithm's running time or space complexity.
• Mathematical Notation: $�(�)$ is $�(�(�))$ if there exist constants $�$ and ${�}_0$ such that $0\le �(�)\le �\cdot �(�)$ for all $�\ge {�}_0$.
• Example:
  • Suppose an algorithm has a time complexity of $�({�}^2)$. This means that the running time grows, at worst, quadratically with the input size $�$.

2. Big Omega (Ω):

• Definition: Big Omega (Ω) notation provides a lower bound or best-case scenario for the growth rate of an algorithm's running time or space complexity.
• Mathematical Notation: $�(�)$ is $\mathrm{\Omega }(�(�))$ if there exist constants $�$ and ${�}_0$ such that $0\le �\cdot �(�)\le �(�)$ for all $�\ge {�}_0$.
• Example:
  • If an algorithm has a time complexity of $\mathrm{\Omega }(�)$, it means that the running time grows, at best, linearly with the input size $�$.

3. Big Theta (Θ):

• Definition: Big Theta (Θ) notation provides both upper and lower bounds, giving a tight range for the growth rate of an algorithm's running time or space complexity.
• Mathematical Notation: $�(�)$ is $\mathrm{\Theta }(�(�))$ if there exist constants ${�}_1,{�}_2$, and ${�}_0$ such that $0\le {�}_1\cdot �(�)\le �(�)\le {�}_2\cdot �(�)$ for all $�\ge {�}_0$.
• Example:
  • Consider an algorithm with a time complexity of $\mathrm{\Theta }(�)$. This implies that the running time grows linearly with the input size $�$ within a tight range.

How It Helps:

• Comparison:
  • Asymptotic notations help compare and contrast algorithms by providing a standardized way to express their efficiency in terms of input size.
• Prediction:
  • They allow you to predict how an algorithm will behave with larger inputs without having to run the algorithm on every possible input.
• Selection:
  • When choosing algorithms for specific tasks, understanding their asymptotic behavior aids in selecting the most efficient one.

Real-World Analogy:

• O(n^2):
  • It's like estimating the maximum time it could take to organize a set of books, even if you have to consider every pair of books.
• Ω(n):
  • It's like knowing that, in the best-case scenario, organizing a set of books will take at least linear time, regardless of how many books there are.
• Θ(n):
  • It's like having a good estimate that organizing a set of books will take somewhere between a linear and quadratic amount of time.

Time-Space Trade-off:

Definition:

Time-space trade-off is a concept in computer science and algorithm design where you analyze the relationship between the amount of time an algorithm takes to execute and the amount of space (memory) it consumes. In many cases, there's an inverse relationship between time and space, meaning you can often achieve better time efficiency at the cost of increased space complexity, and vice versa.

Importance:

1. Resource Optimization:

   • Time-space trade-off allows you to optimize the use of resources (memory and processing power) based on the specific requirements of a given problem or application.

2. System Constraints:

   • Depending on the system constraints (e.g., available memory, processing speed), making appropriate time-space trade-offs becomes essential for efficient operation.

3. Scalability:

   • When designing algorithms for scalable systems, considering time-space trade-offs is critical to ensure that the system can handle increased workloads without significant degradation in performance.

4. User Experience:

   • In user-facing applications, such as mobile or web apps, optimizing for either faster response times or lower resource usage can directly impact the user experience.

Example:

Let's consider a sorting algorithm. A simple algorithm like Bubble Sort may have lower space complexity (uses minimal extra memory), but its time complexity could be higher, especially for large datasets. On the other hand, more advanced algorithms like Merge Sort or QuickSort may use additional memory (space) for improved time efficiency.

Abstract Data Type (ADT):

An Abstract Data Type (ADT) is like a blueprint or a set of instructions for a particular kind of data structure. It defines a set of operations that can be performed on the data, without specifying how those operations are implemented. In simple terms, an ADT tells you what you can do with the data, not how it's done.

Let's Apply ADT to the Example of an Array:

Array as an ADT:

An array is a common data structure used in programming. Let's view it as an ADT:

1. ADT Operation: Insert (Adding an Element)

   • ADT Terminology: Insert(element, index)
   • Description: Add an element at a specified position in the array.

2. ADT Operation: Delete (Removing an Element)

   • ADT Terminology: Delete(index)
   • Description: Remove the element at a specified position in the array.

3. ADT Operation: Access (Retrieving an Element)

   • ADT Terminology: Access(index)
   • Description: Retrieve the element at a specified position in the array.

4. ADT Operation: Search (Finding an Element)

   • ADT Terminology: Search(element)
   • Description: Find the index of a specified element in the array.

How ADT Encapsulation Works for an Array:

• Encapsulation: The array ADT encapsulates the details of how elements are stored, accessed, inserted, deleted, and searched. Users interact with the array through these abstract operations without knowing the internal implementation details.

• Flexibility: The array ADT allows for different implementations (e.g., dynamic arrays, static arrays), but users only need to understand the abstract operations.

Next Page >>